Syntax Diagrams and Parsing

Contents

• Syntax Diagrams
• Coding the Parser
• Parse Trees
• Application to our Monopoly Project

Syntax Diagrams

30 + 40 return

The first step is to write a program that can recognize arithmetic expressions. This kind of program is called a parser.

Before we can write the parser, we have to analyse the structure in arithmetic expressions: the syntax. Let's look at a couple of them:

20
30 + 40 
-6
6/5 + 8
5 * (4+8)
70 + (8*(4-6) * (50 + 50 + 100*44))

Even simpler than numbers are operators:

The big trick is how we combine them into expressions. One thing you notice when looking at a very complicated expression is that it seems to contain other, simpler expressions. We can express this using recursion. Recursive definitions define a concept by using simpler versions of itself. Eventually, we will stumble upon the simplest expression of them all: a number.

It seems loopy, but since every expression inside a big expression is a smaller expression, the process of parsing will eventually terminate. It will terminate once we reach the simplest possible form. This form is called a token.

Tokens are the atoms of the grammar of our language. Almost all programming languages can be decomposed in the way we did it here, i.e. a context free grammar. Sometimes, though, it is very complex. C++ in particular is very very hard to parse. You will learn more details in the compiler construction course next year.

Coding the Parser

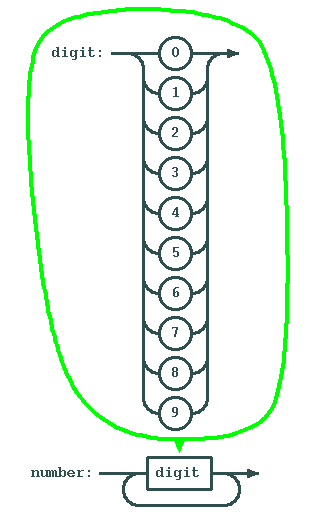
Let's start if the simplest thing: a digit. We will use two primitives: getc() and ungetc(). The idea is simple: we read characters as long as they are what we expect. If a character suddenly is not what we expect, then we put it back so that someone else (who might want this character) can re-read it.

So, here is our function digit():

int digit()
{
  int c = getc(); // getc returns an integer.
  if (c >= '0' && c <= '9')
    return 1;
  else {
    ungetc(c);
    return 0;
  }
}

int number()
{
  if (digit()) {
    while (digit())
      ;
    return 1;
  }
  else return 0;
}

int expression()
{
  // case expression begins with a number.
  if (number()) {
    if (operator()) 
      return expression();
    else
      return 1;

  // case expression begins with something else:
  int c = getc();
  if (c == '-') return expression();
  if (c == '(') {
    if (!expression()) return 0;
    c == getc();
    return (c == ')');
  }
  return 0;  
}

Parse Trees

One data structure that is inherently recursive is the tree. It is therefore ideally suited to represent expressions. In fact, trees are so versatile that it is standard procedure to represent anything governed by a context free grammar by a so called parse tree.

This is how the parse tree of an expression would look like:

The exact details on how to make those trees and how to evaluate them must be left for later, otherwise the compiler construction teacher will be out of his job...

Of interest for us here is that the technique of reading and writing objects in general can become quite complex, and that the basic aim of the monopoly project is to show you how to start doing it. Later, you will be able to consider a whole program as just another object.

Application to our Monopoly Engine

In today's exercise, you will install a new base class with full scale parsing. The Base::read() function will be able to backtrack whenever it finds an object it didn't expect.

Today's other exercise will be to implement the list object. We are now prepared to understand how we will parse a list object, and how we will implement it:

Now we can see how convenient it is to use virtual functions for the contents, and a fixed set of functions for the form. We can concentrate all the ugly code into one module, and emphasize the actual data inside the objects.